越来越多的关键应用都对精确性和计算延迟时间有严格的要求。FPGA的灵活性和性能使得它们广泛应用在工业、科学、军事以及其他的许多应用场合中，来计算复杂的数学问题或者传递函数，有许多算法，比如CORDIC算法，可以用来做为超越函数的计算处理模块。

CORDIC算法可以用来实现正弦、余弦、乘法、除法、平方根等超越函数，因此，把CORDIC算法和基本的数学模块结合起来来计算传递函数，可以得到较为精确的结果。但是，对于复杂的传递函数来说，获得精确结果的代价是花费更多的设计和验证的时间。

对于复杂的传递函数，除了在FPGA中实现精确的函数功能外，还有许多更为有效的处理方法。一个例子就是用FPGA来监控铂电阻温度计（PRT），并把铂电阻温度计的电阻值转换为温度。这个转换一般会使用Callendar-Van Dusen方程，这个方程可以用来确定0℃~660℃之间的温度值，方程如下：

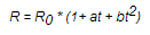
其中R0是0℃时的电阻值，a和b是和PRT相关的系数，t表示温度。事实上，我们是想通过电阻值来转换得到温度值，因此，我们需要重新整理方程，把温度值作为方程的结果。大部分使用PRT的系统会设计一个电路来测量PRT的电阻值，而在FPGA中使用一个重新整理过的，比之前复杂得多的方程来计算温度值，方程如下：

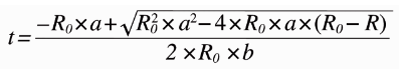
在FPGA中实现这样一个方程，即使是一个经验丰富的FPGA工程师也会感到气馁。通过测试，把电阻值和温度值的对应关系绘图如下：

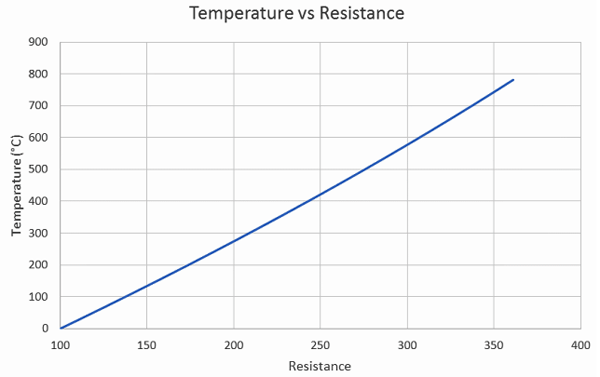
如果仔细研究，会发现这是一个非线性的曲线。

串行外设都会用到RS232-C异步串行接口，传统上采用专用的集成电路即UART实现，如TI、EXAR、EPIC的550、452等系列，但是我们一般不需要使用完整的UART的功能，而且对于多串口的设备或需要加密通讯的场合使用UART也不是最合适的。如果设计上用到了FPGA/CPLD器件，那么就可以将所需要的UART功能集成到FPGA内部，本人最近在用XILINX的XCS30做一个设计的时候，就使用VHDL将UADT的核心功能集成了，从而使整个设计更加紧凑，更小巧、稳定、可靠，下面就谈谈设计方法。

分析UART的结构，可以看出UART主要由数据总线接口、控制逻辑和状态接口、波特率发生器、发送和接受等部分组成，各部分间关系如图一。

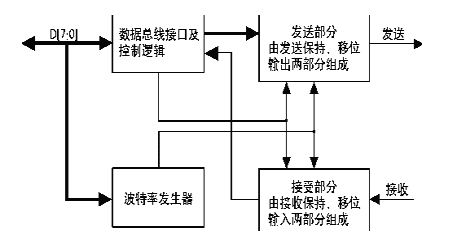
了解了UART的各部分组成结构后，下面对各部分的功能进行详细的分析。我们假定所要设计的UART为：数据位为7位、8位可选，波特率可选，效验方式为奇、偶、无等效验方式，下面的分析都是在这个假定的基础上进行。

一、波特率发生部分

从图一可以看出，UART的接收和发送是按照相同的波特率进行收发的（当然也可以实现成对的不同波特率进行收发），波特率是可以通过CPU的总线接口设置的。UART收发的每一个数据宽度都是波特率发生器输出的时钟周期的16倍，即假定当前按照9600bps进行收发，那么波特率发生器输出的时钟频率应为9600＊16Hz，当然这也是可以改变的，我们只是按照UART的方法进行设计。

我们假定提供的时钟为1.8432MHz，那么可以很简单地用CPU写入不同的数值到波特率保持寄存器，然后用计数器的方式生成所需要的各种波特率，这个值的计算原则就是1843200/（16＊所期望的波特率），如果希望输出9600Hz的波特率，那么这个值就是1843200/（16＊9600）=12（0CH）。

二、 发送部分

这里应重点分析几个问题：首先是何时CPU可以往发送保持寄存器（THR）写人数据？也就是说CPU要写数据到THR时必须判一个状态，当前是否可写？很明显如果不判这个条件，发送的数据会出错，除非CPU写入THR的频率低于当前传输的波特率，而这种情况是极少出现的。其次是CPU写入数据到THR后，何时THR的数据传送到发送移位寄存器（TSR）并何时移位？即如何处理THR和TSR的关系？再次是数据位有7、8位两种，校验位有三种形式，这样发送一个字节可能有9、10、11位三种串行长度，所以我们必须按照所设置的传输情况进行处理。数据位、效验方式可以通过CPU写一个端口来设置，发送和接受都根据这个设置进行，由于这部分很简单，所以我就不给出程序了。

根据上面的分析，引进了几个信号：

bigin1、begin2：引入两个附加移位，目的是为送出起始位、停止位而加入串行长度。

txdone7、txdone8：分别表示7、8位的结束标志。Txdone<=txdone8 when“8bit”else txdone7;

Paritycycle7、paritycycle8：分别表示7、8位下的校验位。Parity<=parity8 when“8 bit”else parity7;

Writerdy：为0时表示CPU不能将数据写入THR，为1时可以写入。

这样就可以得到以下信息：在移位时钟的上升沿检测到txdone和writerdy都为高电平时，进入LOAD状态即将THR的数据LOAD到TSR，在下一个时钟就进入移位状态。在移位中同时进行校验位的运算，在需要送出校验位的时候将运算好的校验位送出，txdone=1的时候将高电平送出，其它时候移位输出。

为了减少设计以及验证的工作，保证项目进度，许多工程师会寻找其它不同的方式来实现这个函数。其中一个方式是利用查找表来保存图表中曲线上的一些点，在这些点之间可以采用线性插值的方式，这个方法可能可以满足需求，但要依赖于精确度的要求以及查找表中能存储的点的个数。但这种方法会引入一个线性插值函数，这个函数通常会包括一个无二次幂限制（non-power-of-two）的除法，这会带来计算的复杂度。

现在的FPGA器件，比如Xilinx Spartan-6、7-系列Atrix、Kintex以及Virtex等FPGA器件中都会包含更多地传统意义上的查找表和触发器。同时也包含内置的DSP slices，Block RAM和一些分散的RAM单元，还有一些象PCIe、以太网端点、高速串行连接等先进的硬IP核，用这些器件可以轻松地实现传递函数。

多项式近似法可以充分利用FPGA器件中丰富的DSP和RAM资源， 使用这项技术，首先要把数学函数用图表来表达，可以用MATLAB或者Excel等数学工具来遍历输入值的范围，然后就可以得到一个多项式趋势线，这样，就可以在FPGA中实现这个方程，而不需要使用电路逻辑直接实现复杂的数序函数，这种趋势线近似方程也可以满足精度的要求。

大部分用来生成多项式趋势线的数学工具都支持选择多项式的介数或者项数，介数越大，精确度就越高，但在FPGA中就需要实现更多的项数。用这种方法通过Microsoft Excel来分析PRT曲线，可以获得4介多项式

一个多项式方程可能不能满足传递函数全部输入范围的精度要求，那么只需要产生更多的多项式方程，通过产生许多多项式常数来覆盖输入范围，一旦输入的值超出了特定的边界，只需要加载一组新的常数值就可以了。上述方法依然是有效的。

假设，我们需要把操作范围扩展到300 ℃，原来的方法就不能满足设计要求了，采用刚刚提到的分段的方法，可以通过绘制269℃ 到300℃之间的趋势线来解决这个问题，这样可以得到另一个多项式方程，该方程可以满足这个输出范围的精度要求。简言之，分段的实现方法在输入值没有超出268℃对应的预定值范围时，采用的是第一组多项式常数，而当输入值超出了268℃对应的预定值范围时，就采用第二组常数来保证精度要求

尽管设计团队使用了内嵌微处理器的片上系统，比如内嵌ARM Cortex-A9 MPCore的Xilinx Zynq可编程SoC器件，但实现传递函数还是具有较大的挑战，首先，通过处理器执行软件来实现传递函数所花的时间要远远大于通过可编程逻辑实现传递函数的运行时间，这样就会使系统响应变慢，事实上，上面提到的传递函数的计算就是一个比较典型的例子，它的数据处理应该通过Zynq SoC器件的可编程逻辑去实现。